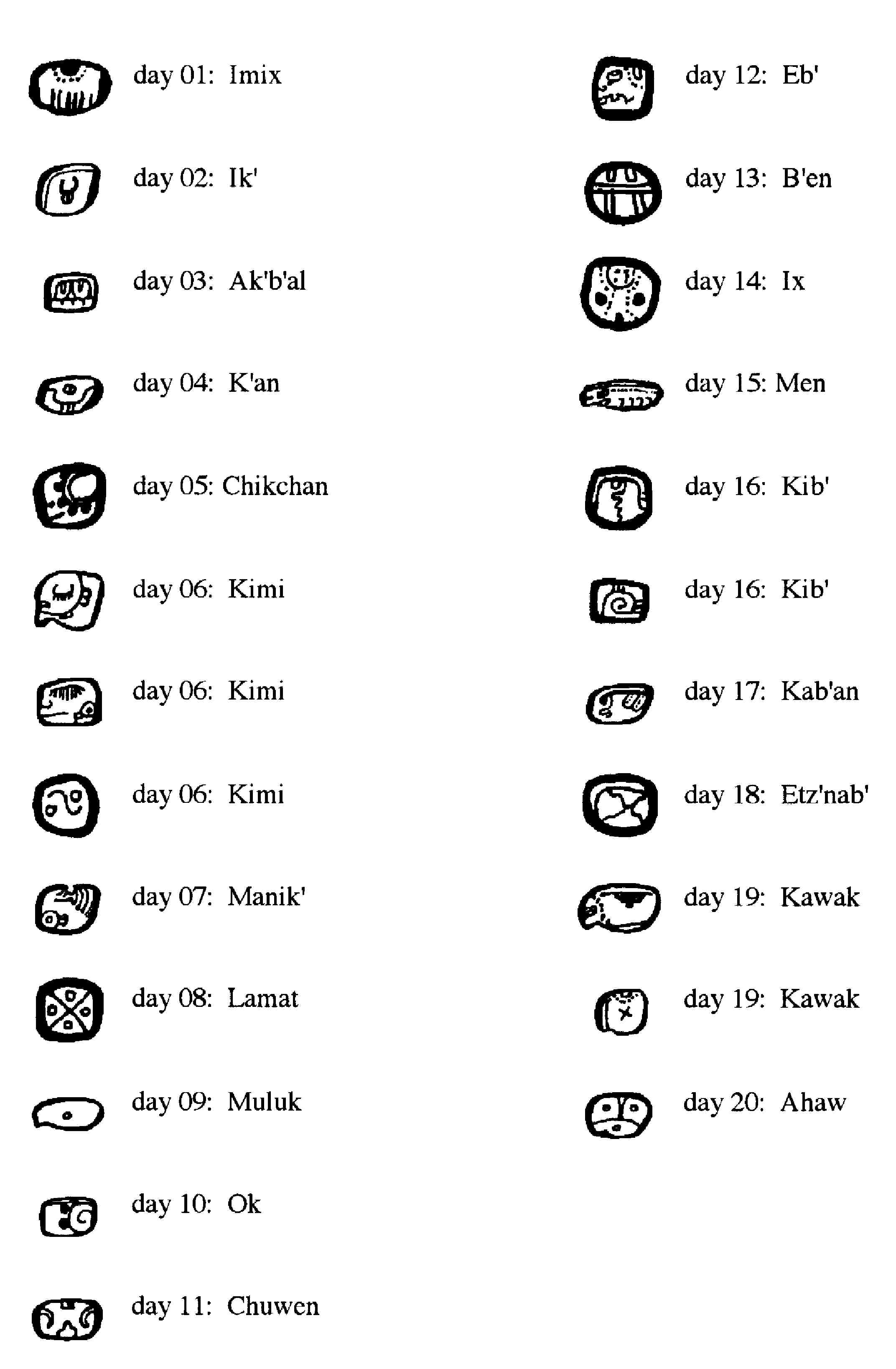
Days of the Maya tzolk'in.
Some of the earliest advances in decipherment were made in terms of interpreting dates recorded in Maya texts. Like other Mesoamerican cultures, the Maya used several independent but overlapping calendars to track time. The first, which is based on a 260-day repeating cycle known as the tzolk'in, functioned primarily as a mechanism for divination and prophecy. A second calendar, the haab', is 365 days in length and is based on the solar year. The two were used concurrently and together created a 52-year cycle. Throughout much of Mesoamerica, the beginning of this 52-year period was celebrated with a number of rituals, including the extinguishing of old fires, the lighting of new fires, the dedication of new temples, and other renovation or renewal ceremonies.
The tzolk'in, or ‘count of days’, plays a significant role in the Maya codices. It consists of 20 named days, represented by the glyphs seen below, and a number (or coefficient) ranging from 1 to 13. Each day may be paired with each coefficient, resulting in a 260-day repeating cycle that begins with the first coefficient (1) and the first day name (Imix). The next day would be 2 Ik’, followed by 3 Ak’b’al, 4 K’an, 5 Chikchan, 6 Kimi, 7 Manik’, 8 Lamat, 9 Muluk, 10 Ok, 11 Chuwen, 12 Eb’, and 13 B’en. Since there are no coefficients above 13, the day following 13 B’en is 1 Ix, followed by 2 Men, 3 Kib’, etc. The last day in the cycle is 13 Ahaw (day 260), after which it starts over again with 1 Imix.
Some of the day glyphs had more than one variant, as can be seen from the illustration (examples include Kimi and Kawak).

Days of the Maya tzolk'in.
The haab' is composed of 18 months of 20 days (represented by the glyphs seen below) and a final month of five days, known as Wayeb’. This creates a period of 365 days, which approximates the seasonal or tropical year of 365.2422 days. The days of the haab' were counted in much the same way as we count the days of our months, except that they were numbered from 0 to 19 during the Classic period and from 1 to 20 during the Late Postclassic and Colonial periods. During the Classic period, the first day of the year corresponded to 0 Pop; this was followed by 1 Pop, 2 Pop, 3 Pop, and so on to the last day of the month (19 Pop). The next month began on 0 Wo, followed by 1 Wo, 2 Wo, etc. The last day of the year corresponded to 4 Wayeb’.

Months of the Maya haab'.
This is the interpretation of the haab' that we follow, but not all epigraphers (those who study Maya hieroglyphic writing) would agree with this analysis. Rather, some believe that the “seating” of a month (indicated by “0” in the preceding paragraph) refers to the twentieth day of the preceding month rather than to the first day of a new month. This interpretation is challenged in a paper presented by Victoria Bricker in 1989 in which she provided compelling evidence in support of the interpretation discussed here.
The tzolk'in and the haab' were combined to create a 52-year period known as the Calendar Round. A Calendar Round designation consists of a tzolk'in date followed by a haab' date—for example, 1 Ahaw 3 Pop. To reach the next date in the series, one moves forward one position in the tzolk'in (to 2 Imix) and one position in the haab'(to 4 Pop). This combination of dates will not occur again until 18,980 days, or 52 years, have passed.
Because of the way the two calendars are structured, only four of the 20 named days can correspond with any particular haab' date. The four days that co-occur with the first day of each year (0 Pop during the Classic period and 1 Pop during the Late Postclassic period) are known as yearbearers. At least three different calendars (incorporating different yearbearer sets) were used in the Maya area at different times in the past. The Classic set pairs the days Ik’, Manik’, Eb’, and Kab’an with 0 Pop (i.e., 1 Ik’ 0 Pop is followed one year later by 2 Manik’ 0 Pop; the following year begins on 3 Eb’ 0 Pop, and the year after that on 4 Kab’an 0 Pop). This is the set that occurs in the Dresden Codex; it may be seen, for example, in the yearbearer almanac on pages 25-28. Another set, known as the Puuc or Campeche yearbearers after the area of the Yucatán peninsula where it was first identified, is based on the days Ak’b’al, B’en, Lamat, and Etz’nab’. A third yearbearer set, named after the site of Mayapán, involves a shift to the days K’an, Muluk, Ix, and Kawak, which are paired with 1, rather than 0, Pop. This system came about by delaying New Year’s day in the Classic period calendar by two days and renaming it 1 Pop. Although the three sets can be seriated chronologically to some extent, they overlap in use at certain sites and certain points in time. Both the Mayapán and Classic period set are represented in the Madrid Codex—the Mayapán yearbearers are featured in the almanacs on Madrid 24c-25c and 34-37, for example, whereas the Classic period set is represented in the almanacs on Madrid 65-73b and Madrid 99b-100b.
In addition to these calendrical cycles, the Maya also made use of a calendar known as the Long Count, which places dates in linear rather than cyclical time. The Long Count calendar was established during the Preclassic era, perhaps by the Olmec, and appears to have been astronomically motivated. The beginning of the current era (August 11, 3114 B.C.) may be linked to a solar zenith passage in the southern Maya area, whereas the end of the era (December 21, A.D. 2012) corresponds to the date of a winter solstice. Although not all Mayanists agree on the best means of correlating the Maya and Christian calendars, the two solutions preferred by most epigraphers today differ from each other by only two days. An overview of the correlation question may be found in The Ancient Maya by Robert Sharer.
The Long Count is based on units of 20, rather than 10 as we use, and is organized as follows: The smallest unit is the k’in, which is equivalent to one day. A winal is equal to 20 k’ins, or 20 days. Rather than consisting of 20 winals, the tun deviates from this system; it is equal to 18 winals, or 360 days, which is a close approximation of the length of the solar year. K’atuns are equal to 20 tuns, or 7200 days (just short of 20 years), whereas b’ak’tuns equal 20 k’atuns (144,000 days), which is almost 400 years in length.
Four symbols are used in the Maya codices to represent the numerals: a shell sign for zero; a dot for one; a bar for five; and a moon sign for 20 (see Figure a below). Numbers from 1-19 may be formed by combining bars and dots as necessary. For larger numbers, however, this system becomes impractical, and positional notation is used instead. Long Count dates in the codices are represented in this manner (Figure b), with the smallest unit (the k’in) appearing at the bottom of the column. A different system of notation is used in the monumental inscriptions, where the units of time (b’ak’tun, k’atun, etc.) are represented by period glyphs. These glyphs may be either symbolic (geometric) in form or expressed by “head variants.” In either case, the coefficient is attached directly to the period glyph, as opposed to the system used in the codices which relies strictly on place-value notation (Figure c).
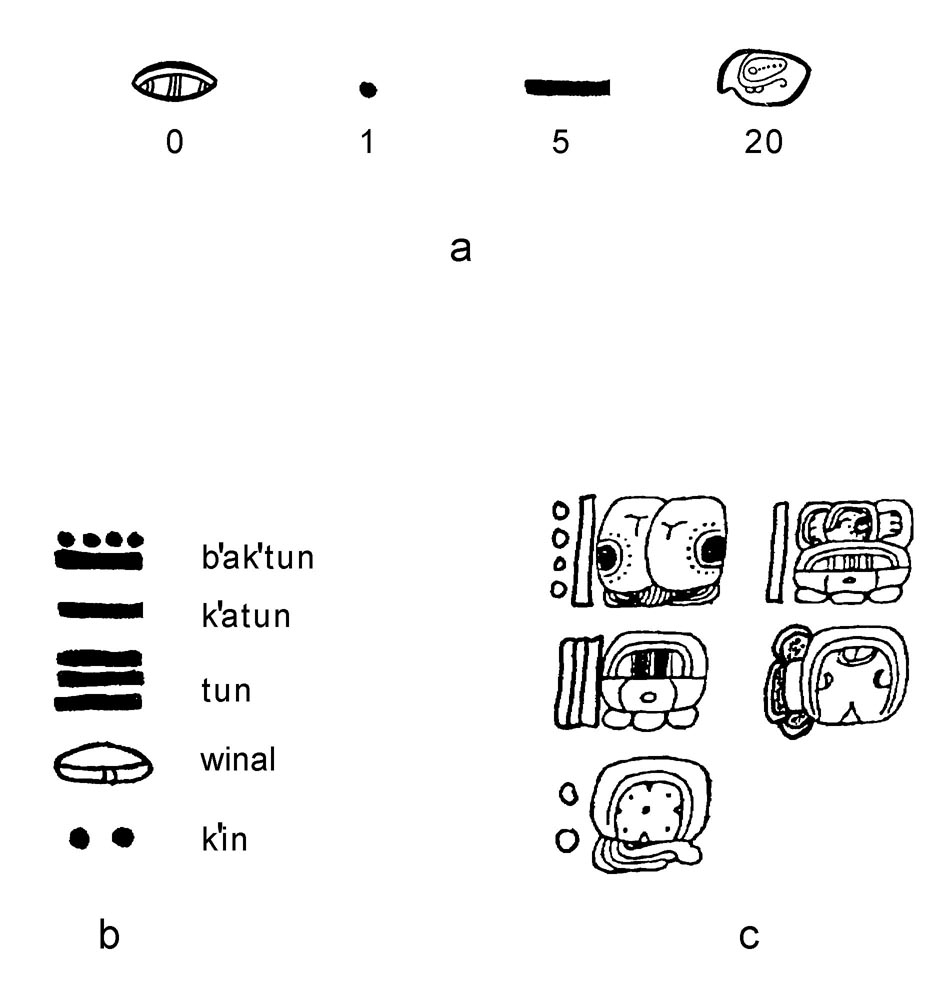
Epigraphers have developed a shorthand convention for writing Long Count dates, which is similar to the abbreviations we use to write dates (e.g., 2/22/01). An example involves the date represented in Figure b, which would be transcribed as 9.5.15.0.2 (with 9 representing the number of b’ak’tuns, 5 the number of k’atuns, 15 the number of tuns , etc.). This corresponds to April 17, A.D. 549 in the Western calendar.
The Long Count is based on a cycle of 13 b’ak’tuns (or 5125 years), which is more than sufficient to account for any event within the recorded history of Maya culture. Long Count dates are generally accompanied by a Calendar Round permutation. For the example given previously (i.e., 9.5.15.0.2), the corresponding Calendar Round date would be 5 Ik’ 5 Wo. Each Long Count date may be associated with one and only one Calendar Round date, although the reverse is not true. The combination of the two defines a date absolutely with reference to a mythological starting date. This date is 13.0.0.0.0 4 Ahaw 8 Kumk’u, or August 11, 3114 B.C. according to the correlation that we use. (The other common correlation places 4 Ahaw 8 Kumk’u on August 13, 3114 B.C.).
Copyright (c) 2002-2013 by Gabrielle Vail, LLC. All Rights Reserved.
Click here for information on how to cite to this website in a publication.